What is the minimum number of races required to determine the fastest 3 horses from a group of 25, given that races can only be conducted among at most 5 horses at a time, and the actual speed of a horse cannot be determined in a race?

Find the fastest 3 horses Puzzle solution
Here is one possible solution to the puzzle of finding the fastest 3 horses from a group of 25:
1. First things first. We will need to race every horse at least once. Any horse left out could be one of the top three. To see every horse in a race, we need 5 races.
25 horses / 5 horses per race = 5 races2. Once the first five races are completed, we will have a winner for each race. Next, we need to organize a race between all the winners to determine the fastest horse among the 25 horses. If the horse wins this race, it will be declared the fastest horse and there won’t be any horse faster. This final race will be the sixth race in total when combined with the first five races.

3. We can arrange the groups in ascending order based on their speed. As we already know the identity of the fastest horse among all horses, we can presume that its group may include other horses that were also among the fastest. This assumption is based on the fact that we only know for sure that those horses finished behind the overall fastest horse. Similarly, the horses in the second group finished after the second fastest horse, and so forth.

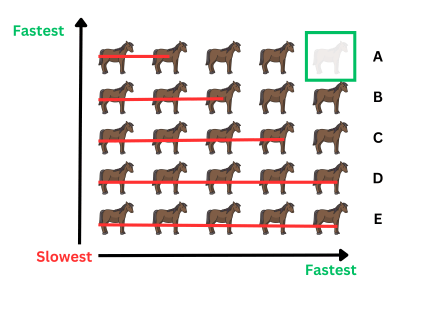
4. With the horses in each group arranged from slowest to fastest (left to right) and the groups arranged from slowest to fastest (bottom to top), we can start removing horses that we know cannot make it to the top three. The basis for this elimination is:
We can make use of the fact that one spot in the top three is already occupied by the overall winner, leaving only two spots left. Using this reasoning, we can conclude that Groups E and D are out of contention. This is because the fastest horse in Group D is four positions behind the overall winner and thus cannot make it to the top three. Similarly, since the lead horse in Group E finished behind the leader in Group D, we can eliminate Group E as well.
This leads us to Group C. It is important to recall that we can utilize the reasoning that the next two horses can only be within any two horses behind the winner. While the leader of Group C has the potential to make it to the top three, being only two positions away from the overall winner, no other horse behind it has a chance.

After eliminating all the horses that cannot make it to the top three, what do we have left?
5. Let’s begin by removing the overall winner from consideration since it has already secured its place in the top three. After this elimination, we are left with a total of five horses. This means we can organize a race with the remaining five horses to determine the final ranking for the top three positions. Please see below.
6. The horses that finish first and second in the final race (the seventh race) will secure the second and third positions in the overall ranking, with the overall winner finishing first. This concludes the process of determining the top three fastest horses.
5 races (all) + 1 race (winners) + 1 race (last five) = 7 races